

- #AREA OF ISOSCELES RIGHT TRIANGLE WITH INTEGRAL HOW TO#
- #AREA OF ISOSCELES RIGHT TRIANGLE WITH INTEGRAL LICENSE#
- #AREA OF ISOSCELES RIGHT TRIANGLE WITH INTEGRAL FREE#
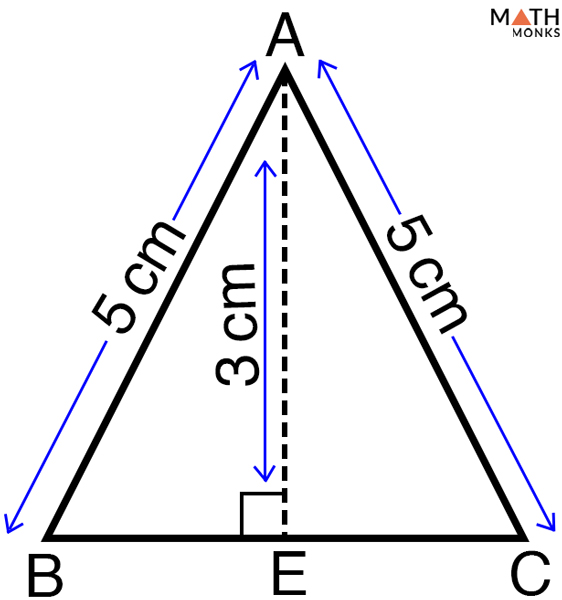
License Agreements, Terms of Use, Privacy Policy. %Y Integers such that: this sequence (the number of even divisors is odd), A028982 (the number of odd divisors is odd), A028983 (the number of odd divisors is even), A183300 (the number of even divisors is even). A194715 (4-cycles in the triangular honeycomb obtuse knight graph), A290391 (5-cycles), A290392 (6-cycles). Isosceles triangle formulas for area and perimeter Given leg a and base b : area (1/4) × b × ( 4 × a - b ) Given h height from apex and base b or h2. %o (Magma) ] // _Vincenzo Librandi_, Apr 30 2011

%C Number of edges of the complete bipartite graph of order 3n, K_] (* _Eric W. (Greetings from The On-Line Encyclopedia of Integer Sequences!) Dx C Question: Find a value x c guaranteed by the Mean Value Theorem of Integration (APEX Calculus, Theorem 42, p. GMAT 740 Story of VuA001105 - OEIS login The OEIS is supported by the many generous donors to the OEIS Foundation. Saturday, July 1,ġ0am NY 2pm London 7:30pm Mumbai
#AREA OF ISOSCELES RIGHT TRIANGLE WITH INTEGRAL FREE#
✅ Subscribe to us on YouTube AND Get FREE Access to Premium GMAT Question Bank for 7 Days ✅ An exceptional GMAT success story of a young Vietnamese student who scored 740 in his third GMAT test attempt - all self study - after the first two failed attempts. Training yourself to look out for unique cases, from the testmaker's perspective, helps you to get a real mastery of the GMAT from a high level.
#AREA OF ISOSCELES RIGHT TRIANGLE WITH INTEGRAL HOW TO#
One of the easiest tricks up the GMAT author's sleeve is to make x equal to a multiple of the radical so that the radical appears on the side you're not expecting and the integer shows up where you think it shouldn't!Īlso, as you go through questions like these, ask yourslf "how could they make that question a little harder" or "how could they test this concept in a way that I wouldn't be looking for it". See all of our video tutorials at Tutorial on how to use integrals to calculate the area of a triangle, something that everyone learn. So.keep in mind that with the Triangle Ratios: People aren't looking for that! And they often won't trust themselves enough to calculate correctly.they'll look at the answer choices and see that 3 of them are Integer*sqrt 2, and they'll think they screwed up somehow because the right answer "should" have a sqrt 2 on the end. I would make a living off of making the shorter sides a multiple of sqrt 2 so that the long side is an integer. If I were writing the test and knew that everyone studies the 45-45-90 ratio as: 1, 1, sqrt 2 Nice solution - just one thing I like to point out on these: Remember, the GMAT doesn't award points for slickness of the math, it awards points for right answers in the shortest amount of time. This is essentially what Squirrel was saying.

And since we're left with just 8 or 16, in this case, plugging in isn't so tough, and we get to 16 in about 31 seconds. It's the only other way the GMAT has ever really made these things hard. You should instantly think - maybe the hypotenuse is the integer. I mean, if the sides were an integer and the hypotenuse were the same integer times root 2, then the perimeter would have to just be 2x + xroot2. But when we try to make it work, it simply doesn't make sense. We know that the triangle has to be x to x to xroot2. Note as well that, in this case, the cross-sectional area is a circle and we could go farther and get a formula for. So, in this case the volume will be the integral of the cross-sectional area at any x x, A(x) A ( x). On this board, with all the practice that everyone's doing, we are all so focused on the various nuances of the GMAT, so this should jump out at you. V lim n n i1A(x i)x b a A(x) dx V lim n i 1 n A ( x i ) x a b A ( x) d x. How do you solve this without backsolving? Solution for The area, A, of an isosceles right triangle varies directly as the square of the length of its leg, /. What is the length of the hypotenuse of the triangle? The perimeter of a certain isosceles right triangle is 16 + 16sqrt(2).


 0 kommentar(er)
0 kommentar(er)
